1.2 알고리즘의 분석

1. 경험적 분석과 수학적 분석

분석은 알고리즘을 정확히 선택하기 위한 방법

시간 소요량 vs 공간소요량

 

- 경험적 분석(Empirical Analysis)

-> 실제 코드를 작성 후, 실행하여 시간을 측정

-> 데이터 수를 다르게 하여 함수관계 유추

 

- 수학적 분석(Mathematical Analysis)

-> 알고리즘 자체를 가지고 수학적인 분석을 함

 

2. 최악의 경우와 최선의 경우

-> 최악의 경우(Worst Case)

가장 많은 시간과 자원을 필요로 하는 경우

-> 최선의 경우 (Best Case)

가장 적은 시간과 자원만이 소요되는 경우

-> 평균적 경우(Average Case)

개념이 모호함

자료의 균일분포? 가장 많은 빈도의 경우?

(적당한 시간과 자원이 소요되는 경우가 아닐까..?)

 

3. 알고리즘 유형

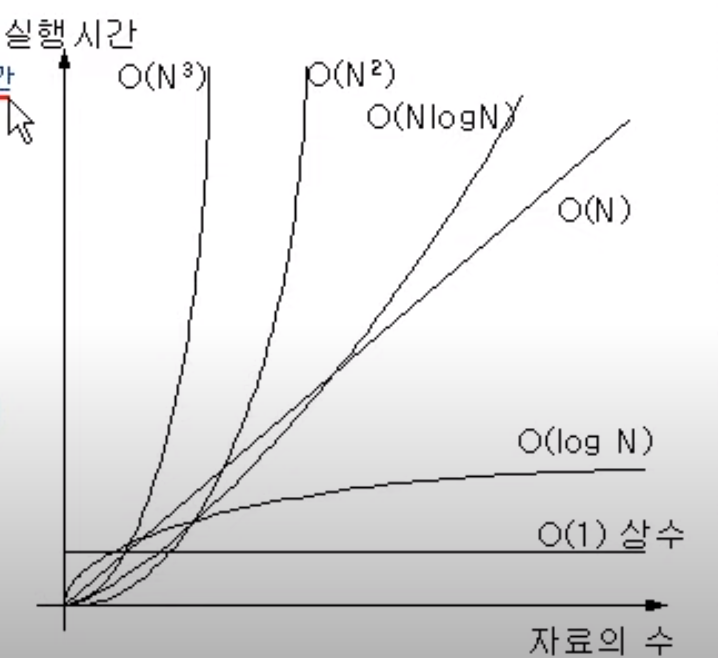
- 1(상수)

입력 자료수와 관계없이 일정한 실행시간

해쉬 검색 알고리즘 등

 

- log N

Divide & Conquer 방법 사용시

이진검색, 이진트리 검색 등

 

- N

Scan 방법 사용시

선형 검색 등

 

- N log N

Divide & Conquer & Merge  방법 사용시

병합정렬 등

 

- N^2

이중 루프

삽입 정렬, 선택 정렬

 

- N^3

삼중 루프

 

 

4-1. 알고리즘 성능 표기법(Big-Oh)

알고리즘의 성능을 객관적으로 표현하는 방법

O표기법(Big-Oh Notation)

-> 실행시간 함수 T(N)이 N0보다 큰 N에 대하여 항상 C0f(n)보다 작거나 같은 C0과 N0가 존재한다면 T(N)은 O(f(N))이라고 한다. 즉, N>=N0인 모든 N에 대하여 T(N)<=C0f(N)이 만족하면 T(N) = O(f(N))임

-> 보통 T(N)에서 가장 영향력있는 항이 선택됨 

ex) T(N) = 3N^2 + 1 이라면 O(N^2)

-> N>=1인 모든 N에 대해 T(N) <= 4N^2

 

4-2. 알고리즘 성능 표기법(Ω, ⊖)

Ω 표기법

-> 실행시간 함수 T(N)이 N0보다 큰 N에 대하여 항상 C0f(N)보다 크거나 같은 C0과 N0가 존재한다면, T(N)은

Ω(f(N)) 이라고 함. 즉, N >= N0인 모든 N에 대해 T(N) >= C0f(N)이 만족하면 T(N) = Ω(f(N))임

 

⊖ 표기법

-> 실행시간 함수 T(N)이 N0보다 큰 N에 대해 항상 C1f(N)보다 크거나 같고, C2f(N)보다 작거나 같은 C1, C2가 존재한다면 T(N)은 ⊖(f(N))이라고 함. 즉, N >= N0인 모든 N에 대해 C1f(N) <= T(N) <= C2f(N)이 만족하면 T(N) = ⊖(f(N))임