논리 회로
01. 불 대수
1. 불 대수
2진수의 값으로 논리적 동작을 취급하는 대수
하나의 변수는 0 또는 1의 값을 가짐
불 대수의 연산자는 논리곱(AND), 논리합(OR), 논리 부정(NOT)이 있음
2. 불 대수의 기본 성질
| 종류 | 논리식 | 종류 | 논리식 |
| 합의 법칙 | X + 0 = X X + 1 = 1 X +X = X X + x̄ = 1 |
곱의 법칙 | X * 0 = 0 X * 1 = X X * X = X X * x̄ = 0 |
| 교환법칙 | X + Y = Y + X X * Y = Y * X |
흡수 법칙 | X + X * Y = X X + x̄ * Y = X + Y X * (X + Y) = X |
| 결합 법칙 | X + (Y + Z) = (X + Y) + Z X * (Y * Z) = (X * Y) * Z |
분배 법칙 | X * (Y + Z) = (X * Y) + (X * Z) X + (Y + Z) = (X + Y) * (X + Z) |
| 대합성의 법칙 |
x̅̅ = x |
드모르간의 법칙 | X+Y(upper bar) = x̄ * Ȳ X * Y(upper bar) = x̄ + Ȳ |
불 대수의 X의 값에 0과 1을 대입할 수 있고, 각각의 값을 대입해보면 다음과 같이 X + 1 = 1의 경우 X에 0 또는 1을 넣으면 0 + 1 = 1, 1 + 1 = 1이 되므로 X + 1 = 1이 됨
3. 논리식의 간략화
논리 함수를 간략화 시키는 방법으로는 불 대수를 이용하는 방법과 카르노 맵을 이용하는 방법이 있음


02. 기본 논리 회로
1. 게이트(Gate)
2진 정보를 처리하기 위한 논리 회로의 기본 소자
입력 논리의 필요 조건을 만족하는 결과(0 또는 1)를 산출
컴퓨터 하드웨어의 기본 소자
(1) AND 게이트
-> 그리고, 논리곱
-> 두 개의 입력값이 모두 1일때만 출력값이 1이 됨

(2) OR 게이트
-> 또는, 논리합
-> 두 개의 입력값 중 하나 이상이 1이면 출력값이 1이 됨

(3) NOT 게이트(=Inverter)
-> ~ 아니다, ~ 않다, 부정을 만드는 논리 연산자
-> 입력값의 반대값이 출력

(4) Buffer 게이트
-> 완충 장치, 버퍼(기억), 완충역의 의미로 Delay(지연)의 개념
-> 입력값 그대로 출력

(5) NAND 게이트
-> NOT + AND, [그리고, 논리곱]의 부정
-> 두 수 중 하나 이상 0이 입력될 때만 1이 출력(AND 결과의 부정)

(6) NOR 게이트
-> NOT + OR, [또는, 논리합]의 부정
-> 두 수 모두 0이 입력될 때만 1이 출력(OR 결과의 부정)

(7) XOR 게이트(eXclusive OR)
-> eXclusive OR, 배타적 논리합
-> 둘 중 하나의 값이 1일 때만(서로 다를 때) 출력값이 1이 됨

(8) XNOR 게이트(=Equivalence)
-> eXclusive NOR, 배타적 부정 논리합(=동치)
-> 두 수 모두 0 또는 1일 때만(같을 때) 출력값이 1이 됨

03. 조합 논리 회로
이전의 입력에 관계없이 현재의 입력값에 의해서만 출력값이 결정되는 회로이며, 기억 기능은 없음
불 대수 조합에 의해 논리적으로 명시되는 정보 처리 동작을 수행
종류 : 반가산기, 전가산기, 감산기, 인코더, 디코더, 멀티플렉서 등
(1) 반가산기(HA; Half Adder)
2진수 1자리(1Bit)의 A와 B를 더한 합(Sum)과 자리올림수(Carry)를 얻는 회로
입력 : 2개(A, B), 출력 : 2개(S, C)
AND 게이트와 XOR 게이트로 구성
<진리표>

<회로도>

진리표에 의해 출력합(Sum)은 배타적 논리합(eXclusive OR)게이트의 진리값이고, 자리올림수(Carry)는 논리곱(AND)의 진리값과 같음
<논리식>

(2) 전가산기(FA; Full Adder)
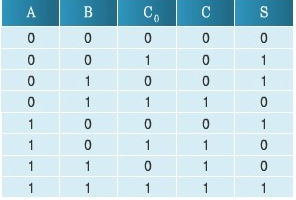
두 비트(A, B)와 전 상태의 자리올림수(C0)를 더해서 합(S)과 최종 자리올림수(C1)를 얻는 회로
입력 : 3개(A, B, C0), 출력 : 2개(S, C1)
2개의 반가산기와 1개의 OR게이트로 구성
<진리표>
<회로도>

<논리식>

(3) 디코더(Decoder, 해독기)
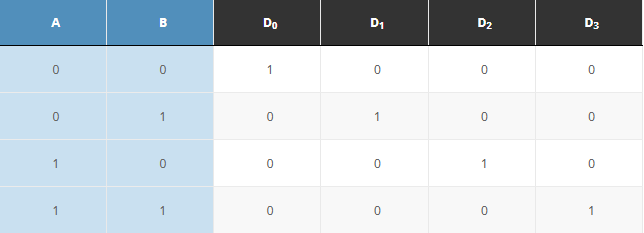
2진 코드 형식의 신호를 출력 신호로 변환시키는 것으로, AND 게이트로 구성
n개의 입력을 받아들여 2^n개의 데이터를 출력
<진리표>
<회로도>

(4) 인코더(Encoder, 부호기)
2^n개의 입력을 받아들여 n개의 데이터를 출력하는 회로이며, OR 게이트로 구성
특정 값을 여러 자리인 2진수로 변환하거나 특정 장치로부터 보내오는 신호를 여러 개의 2진 신호로 변환시키는 장치
(5) 멀티플렉서(Multiplexer, MUX)
2^n개의 입력을 받아들여 하나의 출력선으로 정보를 출력하는 논리 회로
<회로도>

(6) 디멀티플렉서(Demultiplexer)
하나의 입력 신호를 받아들여 2^n개의 출력선 중 하나의 선을 선택하여 출력하는 회로
04. 순서 논리 회로
출력이 입력과 전 상태의 출력에 의해 결정되는 회로
조합 논리 회로와 1비트 기억 소자인 플립플롭으로 구성되며, 기억 능력을 가짐
플립플롭(Flip-Flop) : 1비트('0' 또는 '1')의 정보를 기억할 수 있는 최소의 기억 소자
종류 : RS 플립플롭, JK 플립플롭, D 플립플롭, T 플립플롭 등
(1) RS(Reset/Set) 플립플롭
-> Reset 단자와 Set 단자의 신호에 따라 2진수 한 자리를 기억
-> Reset 단자에만 신호를 보내면 플립플롭의 값은 '0'을 기억
-> Set 단자에만 신호를 보내면 플립플롭의 값은 '1'을 유지
(2) JK(Jack/King) 플립플롭
-> RS 플립플롭에서 S=R=1인 경우에 발생하는 문제점(부정)을 보완/개선한 플립플롭
-> 모든 플립플롭의 기능을 대용할 수 있으므로 응용 범위가 넓고 집적 회로화되어 가장 널리 사용됨
-> J=K=1이 되면 전 상태의 반전(Toggle)이 됨
(3) D(Delay or Data) 플립플롭
-> 입력값과 출력값이 같은 플립플롭
-> 일반적으로 입력 신호를 클록 펄스의 시간 간격만큼 지연(Delay)시켜 출력
-> RS 플립플롭에 인버터(Inverter = NOT 게이트)를 연결한 플립플롭
(4) T(Toggle)플립플롭
-> JK 플립플롭에서 입력 J와 K를 하나로 묶어 T(Toggle)로 표시
-> 입력이 '0'이면 상태 불변, 입력이 '1'이면 전 상태의 보수값. 즉, 원 상태와 보수 상태의 2가지만 서로 전환됨
-> 카운터(Counter)회로로 많이 사용